Часть 2
стр 4
?Задание на полях
стр 5
?Задание на полях
стр 6
?Задание на полях
стр 7
?Задание на полях
стр 8
?Задание на полях
стр 9
?
стр 10
?Задание на полях
стр 11
?Задание на полях
стр 12
стр 13
6_?Задание на полях
стр 14
?Задание на полях
стр 15
?
стр 16
?Задание на полях
стр 17
?Задание на полях
стр 18
?Задание на полях
стр 19
?Задание на полях
стр 20
?
стр 21
стр 22
стр 23
стр 24
Задание на полях
стр 25
Задание на полях
стр 26
?Задание на полях
стр 27
?
стр 28
?Задание на полях
стр 29
?
стр 30
?Задание на полях
стр 31
Задание на полях
стр 32
?
стр 33
Задание на полях
стр 34
Задание на полях
стр 35
стр 38
Вариант 2
стр 39
Вариант 2
стр 40
стр 42
8_?Задание на полях
стр 43
?Задание на полях
стр 44
Задание на полях
стр 45
?
стр 46
10_?Задание на полях
стр 47
7_?
стр 48
?
стр 49
?
стр 50
?
стр 51
стр 52
стр 53
стр 54
?
стр 55
стр 56
стр 57
стр 58
Задание на полях
стр 59
Задание на полях
стр 60
Задание на полях
стр 61
стр 62
Вариант 1
стр 63
Вариант 2
стр 64
Страниски для любознательных
стр 66
?Задание на полях
стр 67
?
стр 68
?Задание на полях
стр 69
?
стр 70
?Задание на полях
стр 71
?
стр 72
?Задание на полях
стр 73
Задание на полях
стр 74
?Задание на полях
стр 75
стр 76
стр 77
стр 78
Задание на полях
стр 79
Задание на полях
стр 80
Странички для любознательных
стр 82
7_?Задание на полях
стр 83
?Задание на полях
стр 84
?
стр 85
?
стр 86
?Задание на полях
стр 87
стр 88
?Задание на полях
стр 89
?Задание на полях
стр 90
?Задание на полях
стр 91
?Задание на полях
стр 92
?Задание на полях
стр 93
Задание на полях
стр 94
?
стр 95
?
стр 96
стр 98
?
стр 99
Задание на полях
стр 100
Задание на полях
стр 101
стр 102
Задание на полях
стр 103
стр 104
Задание на полях
стр 105
Задание на полях
стр 106
Задание на полях
стр 107
Правила о порядке выполнения действийЗадание на полях
стр 108
стр 109
стр 110
стр 111
Математика 3 класс учебник Моро, Волкова 1 часть ответы — страница 63
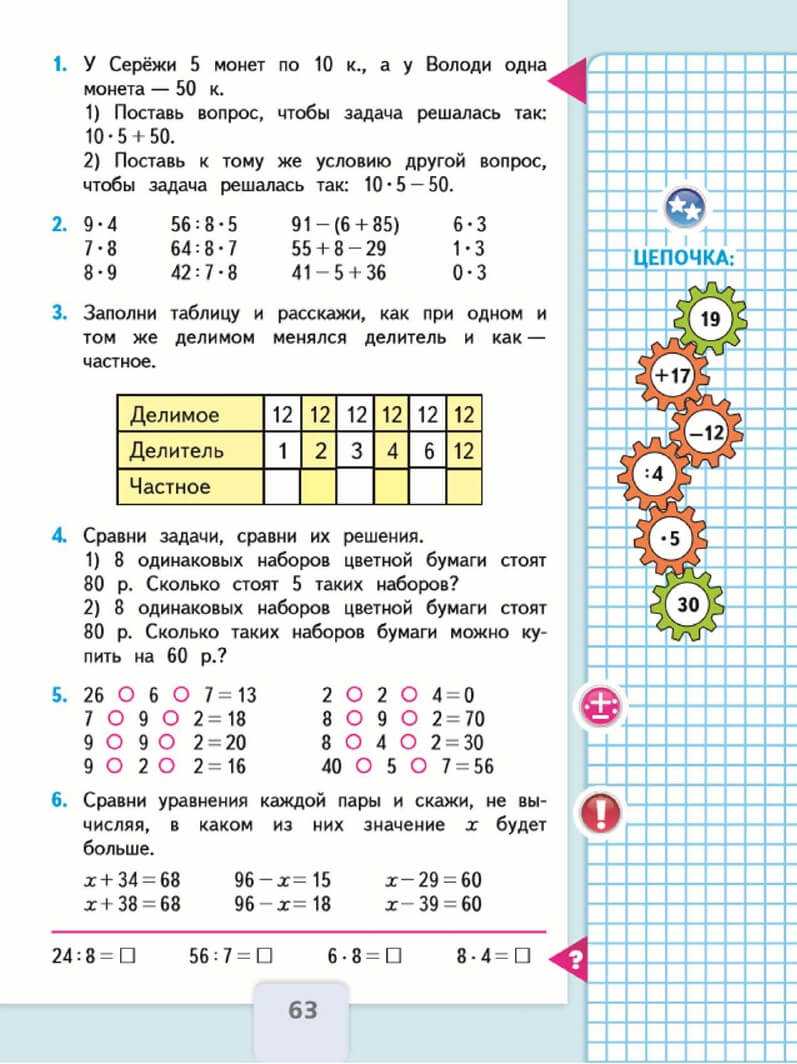
Готовое домашнее задание
У Сережи 5 монет по 10 к., а у Володи одна монета – 50 к. 1) Поставь вопрос, чтобы задача решалась так: 10 ∙ 5 + 50. 2) Поставь к тому же условию другой вопрос, чтобы задача решалась так: 10 ∙ 5 − 50.
Ответ: Задача 1: Сколько всего денег у Серёжи и Володи? 10 ∙ 5 + 50 = 100 (к.) 100 копеек = 1 рубль Ответ: у мальчиков 1 рубль. Задача 2: На сколько денег у Сережи больше, чем у Володи? 10 ∙ 5 − 50 = 0 (к.) Ответ: у них денег поровну.
Ответ: 9 ∙ 4 = 36 6 ∙ 3 = 18 7 ∙ 8 = 56 1 ∙ 3 = 3 8 ∙ 9 = 72 0 ∙ 3 = 0
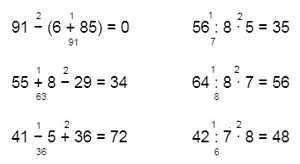
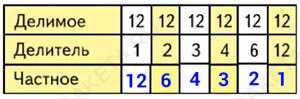
Заполни таблицу и расскажи, как при одном и том же делимом менялся делитель и как — частное.
Ответ:
Сравни задачи, сравни их решения. 1) 8 одинаковых наборов цветной бумаги стоят 80 р. Сколько стоят 5 таких наборов? 2) 8 одинаковых наборов цветной бумаги стоят 80 р. Сколько таких наборов бумаги можно купить на 60 р.?
Ответ: Похожи задачи сюжетом. В обеих неизвестно, сколько стоит 1 набор бумаги. Разница в том, что в первой задаче нужно узнать, сколько стоят 5 наборов (стоимость). А во второй задаче – сколько наборов можно купить (количество). Задача 1:

1) 80 : 8 = 10 (руб.) – стоит один набор. 2) 10 ∙ 5 = 50 (руб.) Ответ: 50 рублей стоит 5 наборов. Задача 2:

1) 80 : 8 = 10 (руб.) – стоит один набор. 2) 60 : 10 = 6 (н.) Ответ: 6 наборов можно купить на 60 рублей.
Ответ:
Сравни уравнения каждой пары и скажи, не вычисляя, в каком из них значение х будет больше.
Ответ: х + 34 = 68 х + 38 = 68 В первом уравнении значение x будет больше, так как второе слагаемое меньше, а значение суммы одинаковое. 96 − х = 15 96 − x = 18 В первом уравнении значение x будет больше, так как уменьшаемое одинаковое, а значение разности меньше. х − 29 = 60 х − 39 = 60 Во втором уравнении значение x будет больше, так как вычитаемое больше, а значение разности одинаковое.
Задание внизу страницы
Ответ: 24 : 8 = 6 56 : 7 = 8 6 ∙ 8 = 48 8 ∙ 4 = 32
Задание на полях страницы
Ответ: 19 + 17 = 36 36 − 12 = 24 24 : 4 = 6 6 ∙ 5 = 30
Числа от 1 до 100 Умножение и деление (продолжение) Площадь. Единицы площади Ответы к стр. 63
1. У Серёжи 5 монет по 10 к., а у Володи одна монета — 50 к. 1) Поставь вопрос, чтобы задача решалась так: 10 • 5 + 50
Сколько всего денег у Серёжи и Володи?
Решение: 10 • 5 + 50 = 100 (к.) О т в е т: у ребят 100 к. или 1 р.
2) Поставь к тому же условию другой вопрос, чтобы задача решалась так: 10 • 5 — 50
На сколько копеек у Серёжи больше, чем у Володи?
Решение: 10 • 5 — 50 = 0 (к.) О т в е т: у ребят денег поровну.
2. 9 • 4 = 36 56 8 • 5 = 35 7 • 8 = 56 64 8 • 7 = 56 8 • 9 = 72 42 7 • 8 = 48
91 — (6 + 85) = 0 6 • 3 = 18 55 + 8 — 29 = 34 1 • 3 = 3 41 — 5 + 36 = 72 0 • 3 = 0
3. Заполни таблицу и расскажи, как при одном и том же делимом менялся делитель и как — частное.
| Делимое | 12 | 12 | 12 | 12 | 12 | 12 |
| Делитель | 1 | 2 | 3 | 4 | 6 | 12 |
| Частное | 12 | 6 | 4 | 3 | 2 | 1 |
4. Сравни задачи, сравни их решения. 1) 8 одинаковых наборов цветной бумаги стоят 80 р. Сколько стоят 5 таких наборов? 2) 8 одинаковых наборов цветной бумаги стоят 80 р. Сколько таких наборов можно купить на 60 р.?
1) 80 8 • 5 = 50 (р.) О т в е т: 5 наборов стоят 50 р.
2) 60 (80 ![]() = 6 (н.) О т в е т: на 60 р. можно купить 6 таких наборов.
= 6 (н.) О т в е т: на 60 р. можно купить 6 таких наборов.
Задачи похожи условием и первым действием. Задачи отличаются вопросом и вторым действием. В первой задаче мы находили стоимость, во второй — количество.
5. 26 — 6 — 7 = 13 2 + 2 — 4 = 0 или 2 • 2 — 4 = 0 7 + 9 + 2 = 18 8 • 9 — 2 = 70 9 + 9 + 2 = 20 8 • 4 — 2 = 30 9 • 2 — 2 = 16 40 5 • 7 = 56
6. Сравни уравнения каждой пары и скажи, не вычисляя, в каком из них значение х будет больше.
х + 34 = 68 и х + 34 = 68 (в первом уравнении значении х будет больше) 96 — х = 15 и 96 — х = 18 (в первом уравнении значении х будет больше) х — 29 = 60 и х — 39 = 60 (во втором уравнении значении х будет больше)
24 8 = 6 56 7 = 8 6 • 8 = 48 8 • 4 = 32
ЗАДАНИЕ НА ПОЛЯХ:
Цепочка:
19 → 36 → 24 → 6 → 30
Часть 1
стр 4
?
стр 5
?
стр 6
?Задание на полях
стр 7
?Задание на полях
стр 8
?Задание на полях
стр 9
?Задание на полях
стр 10
?
стр 11
стр 12
стр 13
стр 14
Задание на полях
стр 15
Задание на полях
стр 16
стр 18
?
стр 19
?Задание на полях
стр 20
?Задание на полях
стр 21
?Задание на полях
стр 22
?Задание на полях
стр 23
?Задание на полях
стр 24
стр 25
?Задание на полях
стр 26
?Задание на полях
стр 27
?Задание на полях
стр 28
стр 29
стр 30
Задание на полях
стр 31
Задание на полях
стр 32
Вариант 1
стр 33
Вариант 2
стр 34
?
стр 35
?Задание на полях
стр 36
?Задание на полях
стр 37
?
стр 38
?Задание на полях
стр 39
?Задание на полях
стр 40
?Задание на полях
стр 41
?
стр 42
?Задание на полях
стр 43
стр 44
?Задание на полях
стр 45
?
стр 46
?Задание на полях
стр 47
?Задание на полях
стр 48
?
стр 49
Странички для любознательных
стр 52
Задание на полях
стр 53
Задание на полях
стр 54
стр 55
стр 57
стр 58
Задание на полях
стр 59
стр 60
Задание на полях
стр 61
?Задание на полях
стр 62
?
стр 63
?Задание на полях
стр 64
?Задание на полях
стр 65
?Задание на полях
стр 66
ЗЗадание на полях
стр 67
?Задание на полях
стр 68
?Задание на полях
стр 69
?Задание на полях
стр 70
стр 71
?
стр 72
?Задание на полях
стр 73
стр 74
стр 75
стр 76
стр 77
стр 78
Задание на полях
стр 79
Задание на полях
стр 80
Вариант 1
стр 81
Вариант 2
стр 82
?Задание на полях
стр 83
?
стр 84
?
стр 85
?
стр 86
?
стр 87
?Задание на полях
стр 88
стр 89
стр 90
стр 92
стр 93
?
стр 94
стр 95
?Задание на полях
стр 96
?
стр 97
Задание на полях
стр 98
стр 99
2х?Задание на полях
стр 100
?Задание на полях
стр 101
Странички для любознательных
стр 102
стр 103
стр 104
Задание на полях
стр 105
Задание на полях
стр 106
Задание на полях
стр 107
25ранички для любознательных
стр 108
стр 109
стр 110
стр 111
ГДЗ учебник по математике 3 класс Моро. Часть 1. Страница 63. Номер №6
Сравни уравнения каждой пары и скажи, не вычисляя, в каком из них значение x будет больше. x + 34 = 68 ; x + 38 = 68 .
96 − x = 15 ; 96 − x = 18 .
x − 29 = 60 ; x − 39 = 60 .
Решение
x + 34 = 68 ; x + 38 = 68 . В обоих уравнениях, чтобы найти x, нужно из суммы вычесть известное слагаемое. Так как суммы одинаковые, то значение x будет больше в том уравнении, где второе слагаемое меньше, то есть в уравнении x + 34 = 68 .
96 − x = 15 ; 96 − x = 18 . В обоих уравнениях, чтобы найти x, нужно из уменьшаемого вычесть разность. Так как в уравнениях уменьшаемые равны, то значение x будет больше в том уравнении, в котором разность меньше, то есть в уравнении 96 − x = 15 .
x − 29 = 60 ; x − 39 = 60 . В обоих уравнениях, чтобы найти x, нужно к разности прибавить вычитаемое. Так как в уравнениях разность одинакова, то значение x будет больше в том уравнении, где вычитаемое больше, то есть в уравнении x − 39 = 60 .





























