Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
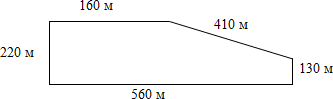
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
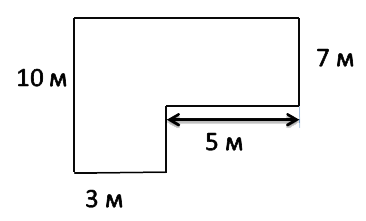
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
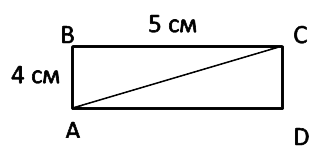
АС — диагональ прямоугольникаABCD. Найдём площадь треугольников
ABC
ACD
Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко
ПрофильБлагодарили:
Сообщений: 1
Ирина Петренко
ПрофильБлагодарили:
Сообщений: 1
как написать правильно площадь треугольника?
Спасибо
Ответить
9 декабря 2015 в 19:41Ответ для Ирина Петренко
Тима Клюев
ПрофильБлагодарили:
Сообщений: 8
Тима Клюев
ПрофильБлагодарили:
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
Спасибо
Ответить
Часть 2:
Урок 1:
1
2
3
4
5
6
7
8
9
10
10
10
11
12
Урок 2:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 3:
1
2
3
4
5
6
7
8
9
10
Урок 4:
1
2
3
4
5
6
7
8
9
10
Урок 5:
1
2
3
4
5
6
7
8
9
10
Урок 6:
1
2
3
4
5
6
7
8
9
10
11
Урок 7:
1
2
3
4
5
6
7
8
9
10
Урок 8:
1
2
3
4
5
6
7
8
9
10
11
Урок 9:
1
2
3
4
5
6
7
8
9
10
11
Урок 10:
1
2
3
4
5
6
7
8
9
10
11
Урок 11:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 12:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 13:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 14:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 15:
1
2
3
4
5
6
7
8
9
10
Урок 16:
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 17:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 18:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 19:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Урок 20:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 21:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 22:
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 23:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Урок 24:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 25:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 26:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 27:
1
2
3
4
5
6
7
8
9
Урок 28:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 29:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 30:
1
2
3
4
5
6
7
8
9
10
Урок 31:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 32:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 33:
1
2
3
4
5
6
7
8
9
10
11
Часть 3:
Урок 1:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 2:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 3:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 4:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 5:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 6:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 7:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 8:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 9:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 10:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 11:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 12:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 13:
1
2
3
4
5
6
7
8
9
10
11
Урок 14:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 15:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 16:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 17:
1
2
3
4
5
6
7
8
9
10
11
Урок 18:
1
2
3
4
5
6
7
8
9
10
Урок 19:
1
2
3
4
5
6
7
8
9
10
Урок 20:
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 21:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Повторение:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
Часть 1:
Урок 1:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 2:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 3:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 4:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 5:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 6:
1
2
3
4
5
6
7
8
9
10
11
Урок 7:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 8:
1
2
3
4
5
6
7
8
9
Урок 9:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 10:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 11:
1
2
3
4
5
6
7
8
9
10
11
Урок 12:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 13:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 14:
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 15:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Урок 16:
1
Урок 17:
1
Урок 18:
1
2
3
4
5
6
7
8
9
10
Урок 19:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 20:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 21:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 22:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 23:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 24:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 25:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 26:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 27:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 28:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 29:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 30:
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 31:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Урок 32:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 33:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 34:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Ход урока
II. Актуализация знаний.
а) Фронтальная работа с сигнальными карточками (у каждого ученика карточки с числами 1, 2, 3, 4; при ответе на вопрос теста ученик поднимает карточку с номером правильного ответа).
1. Квадратный сантиметр – это:
- площадь квадрата со стороной 1 см;
- квадрат со стороной 1 см;
- квадрат с периметром 1 см.
2. Площадь фигуры, изображённой на рисунке, равна:
- 8 дм;
- 8 дм2;
- 15 дм2.
3. Справедливо ли утверждение, что равные фигуры имеют равные периметры и равные площади?
- да;
- нет.
4. Площадь прямоугольника определяется по формуле:
- S = a2;
- S = 2 • (a + b);
- S = a • b.
5. Площадь фигуры изображённой на рисунке, равна:
- 12 см;
- 8 см;
- 16 см.
б) (Постановка проблемы). Задача. Сколько надо краски, чтобы покрасить пол, который имеет следующую форму (см. рис.), если на 1 м2 расходуется 200 г краски?
III. Изучение нового материала.
Что же мы должны узнать, чтобы решить последнюю задачу? (Найти площадь пола, который имеет вид «сложной фигуры».)
Учащиеся формулируют тему и цели урока (если необходимо учитель помогает).
Рассмотрим прямоугольник ABCD. Проведём в нем линию KPMN, разбив прямоугольник ABCD на две части: ABNMPK и KPMNCD.
Чему равна площадь ABCD? (15 см2)
Чему равна площадь фигуры ABMNPK? (7 см2)
Чему равна площадь фигуры KPMNCD? (8 см2)
Проанализируйте полученные результаты. (15= = 7 + ![]()
Вывод? (Площадь всей фигуры равна сумме площадей её частей.)
Как можно применить это свойство для решения нашей задачи?(Разобьём сложную фигуру на части, найдём площади частей, затем площадь всей фигуры.)
Давайте составим план решения задач на нахождение площади «сложной фигуры»:
- Разбиваем фигуру на простые фигуры.
- Находим площади простых фигур.
а) Задача 1. (коллективное решение на доске и в тетрадях.) Сколько потребуется плитки, чтобы выложить площадку следующих размеров:
Решение:
Есть ли другой способ решения? (Рассматриваем предложенные варианты.)
Ответ: 2100 дм2.
Задача 2. (коллективное решение на доске и в тетрадях.) Сколько требуется м2 линолеума для ремонта комнаты, имеющей следующую форму:
Решение:
Ответ: 8 м2.
Физкультминутка.
б) Самостоятельная работа (обучающего характера).
Учащиеся разбиваются на группы (№ 5–8 более сильные). Каждая группа – ремонтная бригада.
Задание бригадам: определите, сколько надо краски, чтобы покрасить пол, имеющий форму фигуры, изображённой на карточке, если на 1 м2 требуется 200 г краски.
Вы эту фигуру строите своей тетради и записывая все данные, приступаете к выполнению задания. Можете обсуждать решение (но только в своей группе!). Если какая-то группа справляется с заданием быстро, то ей – дополнительное задание (после проверки самостоятельной работы).
Задания для групп:
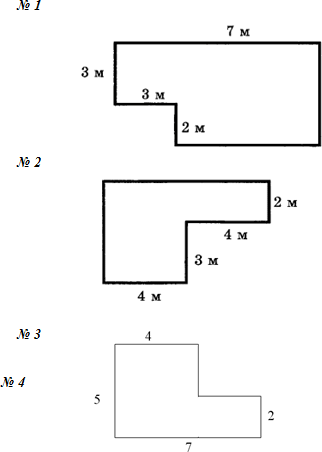
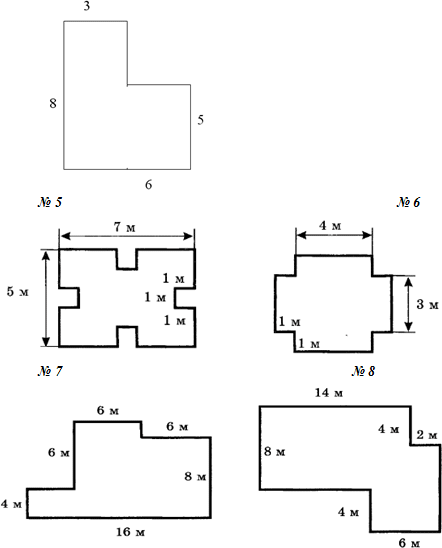
п. 18, № 718, № 749.
Дополнительное задание. План-схема Летнего сада (Санкт-Петербург). Вычислить его площадь.