Олимпиада по математике.Тест. 6-8 классы. Ответы.
1. Газетный лист сложил пополам 5 раз, каждый раз меняя направление сгиба. Затем отрезали от получившегося прямоугольника 4 угла и развернули лист. Сколько в нём дырок?
(A) 21 (В) 25 (С) 32 (D) 45 (Е) 60
2. Периметр квадрата увеличили на 10%. На сколько процентов увеличилась площадь квадрата?
(A) 10% (В) 11% (С) 20% (D) 21% (Е) 50%
3. Пять человек сидят за круглым столом. Каждый из них говорит: «Оба мои соседа — лжецы». Сколько лжецов за столом?
(A) 1 (В) 2 (С) 3 (D) 4 (Е) 5
4. 3 утки и 2 селезня вместе весят 32 кг, 4 утки и 3 селезня весят 44 кг. Сколько весят 2 утки и 1 селезень?
(A) 20 (B) 21 (C) 24 (D) 26 (E) 25,5
5. Имеется 100 маленьких одинаковых кубиков. Из них сооружается самый большой из возможных кубиков. Сколько маленьких кубиков осталось неиспользованными?
(A) 73 (В) 36 (С) 19 (D) 9 (Е) 0
6. Рассказывая о своём дедушке, Оля каждый раз старалась назвать его по-новому: «отец брата отца», «брат отца брата», «отец отца брата», «брат отца отца». Сколько раз Оля ошиблась? (Все братья — родные!)
(A) 0 (В) 1 (С) 2 (D) 3 (Е) 4
7. Перед входом в крепость сложена пирамида из одинаковых пушечных ядер (в основании — правильный треугольник, и ядра каждого следующего слоя лежат в ямках предыдущего слоя). Каким может быть количество ядер в этой пирамиде?
(A) 200 (В) 210 (С) 220 (D) 250 (Е) 256
8. У пиратов в ходу монеты в 1, 2 и 5 пиастров. В кармане у Флинта 10 пиастров. Тогда число монет у него в кармане не может быть равно
(A) 3 (В) 4 (С) 6 (D) 7 (Е) 8
9. Какое из чисел не может быть представлено в виде суммы двух квадратов?
(A) 13 (В) 25 (С) 61 (D) 83 (Е) 101
10. Сколько различных результатов можно получить, расставляя скобки в выражении 10 – 5 – 3 – 1?
(A) 4 (В) 5 (С) 6 (D) 7 (Е) 8
11. Максим родился в воскресенье 29 февраля. Через сколько лет его день рожденья в первый раз снова будет в воскресенье 29 февраля?
(A) 4 (В) 8 (С) 20 (D) 28 (Е) 29
12. Три лыжника, Яша, Федя и Коля, стартовали в таком порядке: Я, Ф, К, то есть сначала Яша, потом Федя, потом Коля. На дистанции Яшу обогнали 3 раза, Федю — 5 раз, а Колю — 8 раз. В каком порядке лыжники пришли к финишу?
(A) Ф, К, Я (В) Я, К, Ф (С) К, Ф, Я (D) Я, Ф, К (Е) нельзя определить
13. В корзине сидят котята — 4 чёрных, 2 рыжих и 1 полосатый. Сколькими способами можно выбрать трёх котят разной окраски?
(A) 4 (В) 5 (С) 6 (D) 7 (Е) 8
14. Произведение возрастов Машиных братьев равно 1664. Младший из братьев вдвое моложе старшего. Сколько у Маши братьев?
(A) 2 (B) 3 (C) 4 (D) 5 (E) 6
15. В шахматном турнире участвовало 8 игроков и каждый с каждым сыграл по одной партии. Сколько всего партий было сыграно?
(A) 28 (В) 36 (С) 49 (D) 56 (Е) 64
Ответы:
|
1 |
А |
||||
|
2 |
D |
||||
|
3 |
С |
||||
|
4 |
А |
||||
|
5 |
В |
||||
|
6 |
С |
||||
|
7 |
С |
||||
|
8 |
А |
||||
|
9 |
D |
||||
|
10 |
А |
||||
|
11 |
D |
||||
|
12 |
D |
||||
|
13 |
E |
||||
|
14 |
В |
||||
|
15 |
А |
По теме: методические разработки, презентации и конспекты
Олимпиады по математике, русскому языку, окружающему миру. Протокол олимпиады.
Материалы олимпиад для 3 класса. Готовый шаблон протокола олимпиад.
Диплом победителя VII онлайн-олимпиады по математике «Олимпиада «Плюс»», декабрь 2017
Диплом победителя VII онлайн-олимпиады по математике «Олимпиада «Плюс»», декабрь 2017.
Диплом победителя VII онлайн-олимпиады по математике «Олимпиада «Плюс»», апрель 2018
Диплом победителя VII онлайн-олимпиады по математике «Олимпиада «Плюс»», апрель 2018.
Диплом победителя VIII онлайн-олимпиады по математике «Олимпиада «Плюс»», апрель 2018
Диплом победителя VIII онлайн-олимпиады по математике «Олимпиада «Плюс»», апрель 2018.
Диплом победителя VIII онлайн-олимпиады по математике «Олимпиада «Плюс»», 2, апрель 2018
Диплом победителя VIII онлайн-олимпиады по математике «Олимпиада «Плюс»», 2, апрель 2018.
Диплом победителя VIII онлайн-олимпиады по математике «Олимпиада «Плюс»», 3, апрель 2018
Диплом победителя VIII онлайн-олимпиады по математике «Олимпиада «Плюс»», 3, апрель 2018.
Диплом победителя VIII онлайн-олимпиады по математике «Олимпиада «Плюс»», 4, апрель 2018
Диплом победителя VIII онлайн-олимпиады по математике «Олимпиада «Плюс»», 4, апрель 2018.
-
Паровозик аппликация для детей 5 6 лет в детском саду
-
Детям о москве в детском саду рассказ
-
Конкурс по риторике в детском саду
-
Когда откроются детские сады в москве
- Деревья для оформления музыкального зала в детском саду
Предварительный просмотр:
Олимпиада по математике
Школьный этап олимпиады – юниор для младших школьников 2013 – 2014 учебный год
- Рысь съедает 600 кг мяса за 6 часов, а тигр – в 2 раза быстрее. За какое время они съедят это мясо вместе?
- В шахматном турнире участвовали 7 человек. Каждый с каждым сыграл по одной партии. Сколько всего партий они сыграли?
- В записи 8 8 8 8 8 8 8 8 поставь между некоторыми цифрами знак сложения так, чтобы получилось выражение, значение которого равно 1000.
- По столбу высотой 6 м ползёт вверх улитка. За день она поднимается на 4 м, за ночь спускается на 3 м. сколько времени ей понадобиться, чтобы добраться до вершины?
- Три брата поймали 29 карасей. Когда один брат отложил для ухи 6 штук, другой 2, а третий – 3, то у каждого осталось равное количество рыб. Сколько карасей поймал каждый из них?
- Найди периметр прямоугольника, состоящего из трех квадратов. Сторона одного квадрата 6 сантиметров, а двух других квадратов по 3 сантиметра.
- Игорь стоит в хороводе. Пятый слева от Игоря тот же, что и шестой справа. Сколько людей в хороводе?
- Два мальчика собирали кедровые шишки. Один у другого спросил:
— Сколько ты собрал шишек?
— Посчитай, — ответил другой, — если это число уменьшить в 7 раз и полученный результат уменьшить на 7, то получится 7. (4 балла)
- Из 10 студентов, прибывших на практику в Англию, 6 говорят по-английски, 7 – по-немецки. Сколько студентов говорят на обоих этих языках? ( 3 балла)
Ответы к стр. 35
152. У круглого стола поставили четыре стула. Сколькими способами можно рассадить на эти стулья:
а) четырёх детей; б) трёх детей; в) двух детей?
а) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, третий ребёнок может сесть на любой из двух оставшихся стульев, четвёртый ребёнок может сесть только на один оставшийся стул , то есть имеется 4 • 3 • 2 • 1 = 24 возможных способа рассадить четырёх детей на стулья.
б) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, третий ребёнок может сесть на любой из двух оставшихся стульев, один стул остаётся свободным, то есть имеется 4 • 3 • 2 = 24 возможных способа рассадить трёх детей на стулья.
в) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, два стула остаются свободными, то есть имеется 4 • 3 = 12 возможных способа рассадить двух детей на стулья.
153. Мальчика и двух девочек надо рассадить за круглым столом с четырьмя стульями так, чтобы девочки не оказались рядом. Сколькими способами это можно сделать?
Чтобы девочки не оказались рядом, между ними, с одной стороны должен сидеть мальчик, а с другой стороны — находиться пустой стул.
Мальчик может сесть на любой из четырёх стульев, первая девочка может сесть на любой из двух оставшихся стульев рядом с мальчиком (но только не напротив него), вторая девочка может сесть на оставшийся стул рядом с мальчиком (но только не напротив него), то есть имеется 4 • 2 • 1 = 8 возможных способов рассадить детей.
154. Двух мальчиков и двух девочек надо рассадить за круглым столом с четырьмя стульями так, чтобы девочки не оказались рядом. Сколькими способами это можно сделать?
Чтобы девочки не оказались рядом, между ними, с одной стороны должен сидеть мальчик, и с другой стороны тоже сидеть мальчик.
Первая девочка может сесть на любой из четырёх стульев, первый мальчик может сесть на любой из двух оставшихся стульев рядом с девочкой (но только не напротив неё), вторая девочка может сесть на стул рядом с мальчиком и напротив первой девочки, второй мальчик может сесть на оставшийся стул, то есть имеется 4 • 2 • 1 • 1 = 8 возможных способов рассадить детей.
155. Бросили два игральных кубика. На первом выпало 3 очка, на втором — 6 очков. (рис. 14). Сколькими разными способами может выпасть сумма в 9 очков? Сколькими различными способами могут выпасть очки на этих кубиках?
Сумму 9 можно получить: 3 + 6 и 4 + 5. На первом кубике может выпасть любое из четырёх чисел (3, 4, 5 или 6), на втором кубике может выпасть только одно число, дополняющее число, выпавшее на первом кубике до суммы, равной 9 (3 + 6, 6 + 3, 4 + 5, 5 + 4), то есть имеется 4 • 1 = 4 возможных способа получить сумму в 9 очков.
На первом кубике может выпасть любое из шести чисел, на втором кубике может также выпасть любое из шести чисел, то есть имеется 6 • 6 = 36 возможных способов.
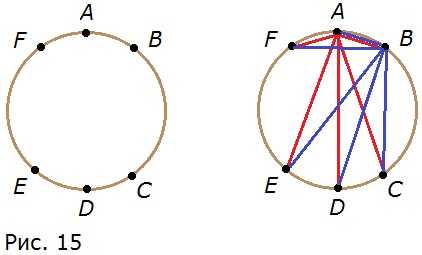
156. а) На окружности отметили 6 точек (рис. 15). Сколько получится отрезков, если соединить каждую точку с каждой?
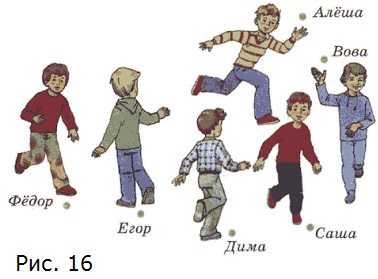
б) Встретились шесть друзей (рис. 16), каждый пожал руку каждому. Сколько было рукопожатий?
а) Из точки А выходит 5 отрезков. Из точки В выходит тоже 5 отрезков, но отрезок ВА — это тот же отрезок АВ. Если продолжить построение отрезков, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (6 • 5) 2 = 15 отрезков.
б) Алёша пожал руку Фёдору, Егору, Диме, Саше и Вове — всего 5 рукопожатий. Фёдор пожал руку Алёше, Егору, Диме, Саше и Вове — всего тоже 5 рукопожатий. Но рукопожатие Алёша-Фёдор и Фёдор-Алёша — это одно рукопожатие. Если продолжить рассматривать рукопожатия, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (6 • 5) 2 = 15 рукопожатий.
157. Восемь друзей решили провести турнир по шашкам так, чтобы каждый сыграл с каждым одну партию. Сколько партий будет сыграно?
Всего 8 друзей, значит, каждый сыграет одну партию с каждым из семи оставшихся друзей. Но, например, если Витя сыграет с Лёшей и Лёша сыграет с Витей — это одна и та же партия. Если продолжить рассматривать количество сыгранных партий, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (8 • 7) 2 = 28 партий.
| ← Предыдущая | Следующая → |























